The formula for the area of an ellipse is a mathematical formula used to calculate the area of an ellipse. It is determined by the semi – major axis and semi – minor axis of the ellipse. The formula for the area of an ellipse is πab, where a and b are the semi – major axis and semi – minor axis of the ellipse, respectively.
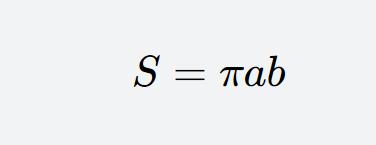
An ellipse is a geometric figure on a plane, and its shape is similar to a stretched circle. The semi – major axis and semi – minor axis of an ellipse are the two main axes of the ellipse, and their lengths determine the size and shape of the ellipse. The formula for the area of an ellipse is πab, where π is the circumference ratio, and a and b are the semi – major axis and semi – minor axis of the ellipse, respectively. To calculate the area of an ellipse, you only need to substitute the values of a and b into the formula.
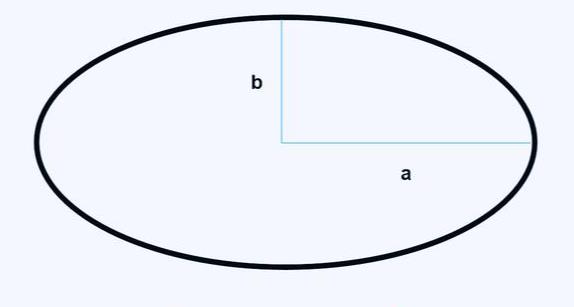
Suppose the semi – major axis of an ellipse is 6 and the semi – minor axis is 4, then its area can be calculated using the formula for the area of an ellipse. According to the formula S = πab, substituting a = 6 and b = 4, we get S = 24π, which is approximately 75.4. Therefore, the area of this ellipse is approximately 75.4 square units.
An ellipse is a geometric figure on a plane, and its shape is similar to a stretched circle. The semi – major axis and semi – minor axis of an ellipse are the two main axes of the ellipse, and their lengths determine the size and shape of the ellipse. The formula for the area of an ellipse is πab, where π is the circumference ratio, and a and b are the semi – major axis and semi – minor axis of the ellipse, respectively. To calculate the area of an ellipse, you only need to substitute the values of a and b into the formula.
The proof of the formula for the area of an ellipse can be completed by the method of integration.
First, we express the equation of the ellipse as x²/a² + y²/b² = 1, where a and b are the semi – major axis and semi – minor axis of the ellipse, respectively. Then, we can divide the ellipse into countless small rectangles, and the area of each rectangle is dS = dx * dy.
Next, we can express dS in the form of polar coordinates, that is, dS = r * dr * dθ, where r and θ are the radius and angle in polar coordinates, respectively. Express x and y in the form of polar coordinates, that is, x = a * cosθ, y = b * sinθ, and substitute them into the expression of dS, we get dS = ab * cosθ * sinθ * dθ * dr.
Finally, we can integrate dS to get the area S of the ellipse, that is, S = ∫∫dS = ∫₀²π∫₀ᵃ b * cosθ * sinθ * dr * dθ = πab. Therefore, the formula for the area of an ellipse is proved.