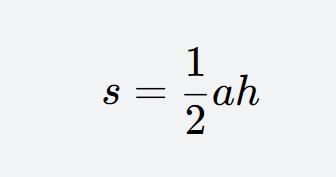In the field of mathematics, it is generally believed that there are different formulas for the area of a triangle depending on the known conditions. For example, the base times height formula, Heron’s formula, sine and cosine formulas, angle bisector formula, and basic formulas such as the sum of angles formula can be used. Additionally, based on different application scenarios and known conditions, various indirect methods for calculating the area of a triangle can be derived from these basic formulas, which are elaborated in relevant literature. This article focuses on the commonly used formulas for calculating the area of a triangle in the industry.
I. Classical Base Times Height Formula
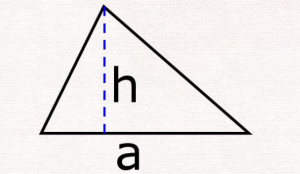
The base times height formula is applicable to triangles where the height corresponding to an angle and the lengths of the two adjacent sides are known. The formula is:
Triangle Area Formula
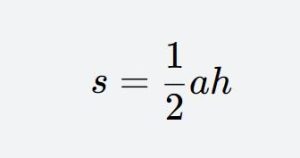
where a represents the base length of the triangle, h represents the height (on the base a), and S represents the area of the triangle.
2.Heron’s Formula (Three-Side Method)
Heron’s formula is applicable to triangles with known side lengths. The formula is:
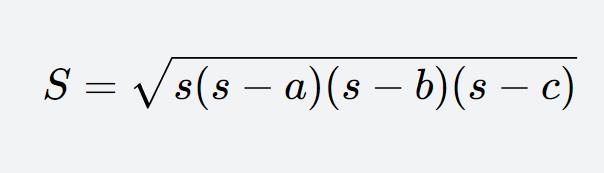
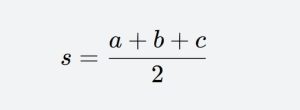
Where s is the semi-perimeter of the triangle, a, b, and c are the lengths of its three sides, and S is the area.
Example: Suppose there is a triangle with side lengths 3, 4, and 5, then Heron’s formula can be used to calculate its area. First, compute the value of s:s=23+4+5=6
3. Using the Sine Formula and Cosine Formula (Method for Two Sides and Included Angle)
The sine formula and cosine formula are applicable to triangles where two sides and the included angle are known. The formulas are as follows:
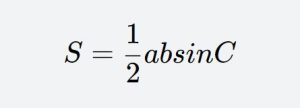
where a and b are the lengths of the two sides, C is the degree measure of the included angle, and sinC is the sine value of angle C.
It can also be written as:
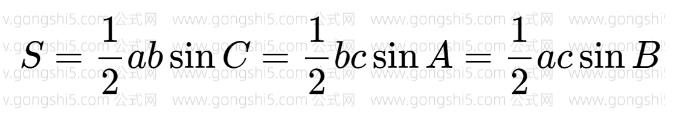
Using the Law of Cosines, we can first find the lengths of the three sides of the triangle. Then, calculate the semi-perimeter using Heron’s formula, and finally substitute it into the triangle area formula to obtain the area of the triangle.