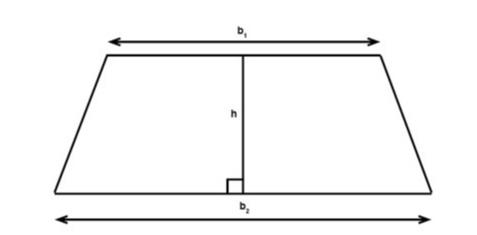
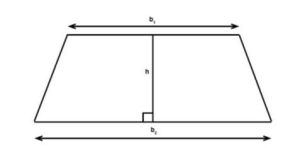
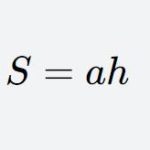The formula for the area of a trapezoid is a mathematical formula used to calculate the area of a trapezoid. A trapezoid is a quadrilateral where the two parallel sides are called the bases of the trapezoid, the two non-parallel sides are called the legs, and the height of the trapezoid is the perpendicular distance between the two bases. The formula for the area of a trapezoid can be expressed as S = 1/2(a + b)h, where a and b are the lengths of the two bases of the trapezoid, and h is the height of the trapezoid. This formula can be derived by decomposing the trapezoid into two triangles and a rectangle.

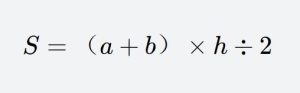
In practical applications, the trapezoid area formula is often used to calculate the area of objects with various shapes, such as roofs in architecture, beams and slabs in engineering, etc. In addition, the trapezoid area formula can also be used to calculate physical quantities such as the center of gravity and moment of inertia of a figure.

Regarding the area of a trapezoid, here is an important historical case. In Elements by the ancient Greek mathematician Euclid, he used the concept of the area of a trapezoid to prove the Pythagorean theorem. He decomposed a square into four trapezoids, then rearranged these trapezoids to form a square with side length c and two trapezoids with areas ab and c2 – ab respectively, thereby obtaining the proof of the Pythagorean theorem, i.e., c2=a2+b2. This proof method is called the Euclidean proof and has become one of the most important achievements in ancient Greek geometry.

When using the trapezoid area formula to calculate the area of a trapezoid, the following points should be noted:

A trapezoid is a quadrilateral with two parallel sides, which are called the bases, and the other two non-parallel sides are called the legs. The height of a trapezoid is the perpendicular distance between the two bases, that is, the perpendicular distance from one base to the other. Trapezoids can have different shapes and sizes, but their two bases must be parallel.

Trapezoids are widely used in mathematics, geometry, and physics. In conclusion, the trapezoid area formula is an important tool for calculating the area of a trapezoid and can be used in various practical applications. When using this formula, attention should be paid to units, accurate measurement of lengths, and decomposition calculation of irregular trapezoids to ensure the accuracy of the calculation results.