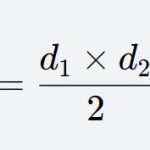An equilateral triangle refers to a triangle with three sides of equal length. It is a special type of isosceles triangle: all three sides are equal in length, all three angles are equal and each angle is 60 degrees. It has symmetry and stability, and its area formula can be derived by dividing the equilateral triangle into two isosceles triangles. Here are two methods to calculate the area of an equilateral triangle:
- Side length calculation method (only the side length is known):
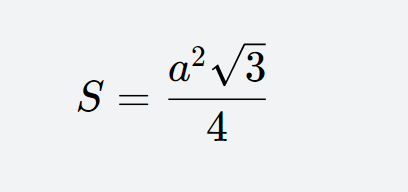
The area formula of an equilateral triangle is: the square of the side length multiplied by the square root of 3 and then divided by 4, that is, S = (a² * √3) / 4, where a is the side length of the equilateral triangle.
- Height calculation method (only the height is known):
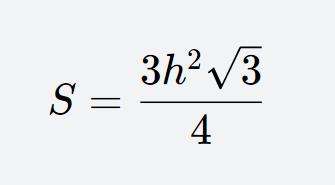
For the height calculation method, the area of an equilateral triangle is equal to 3 times the square of the height multiplied by the square root of 3 and then divided by 4. The formula is S = (3h²√3)/4, where S represents the area, h represents the height, and √3 represents the square root of 3.
Since the height of an equilateral triangle is also its median and altitude, the height can be calculated by dividing the equilateral triangle into two isosceles triangles.
Special points of an equilateral triangle such as the height, median, angle bisector, orthocenter, circumcenter, incenter, and centroid all coincide at the centroid of the triangle.
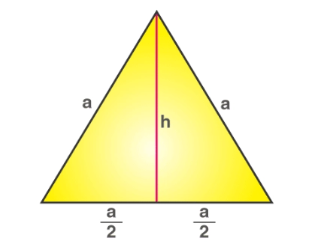
For area calculation, the side length calculation method is more common, and the formula of the side length calculation method can be derived by dividing the equilateral triangle into two isosceles triangles.