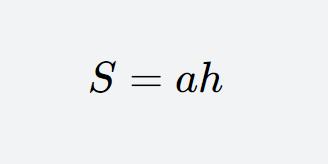A parallelogram is a quadrilateral with four sides, where two adjacent sides are parallel. In other words, it is a four-sided figure with opposite sides that are both parallel and equal in length. A parallelogram can be described by the lengths of its two adjacent sides and the included angle between them. www.mathformula.top provides two classic formulas for calculating the area of a parallelogram, as follows:
1. Base-height calculation method
Base-height calculation method: The area formula of a parallelogram is S = ah
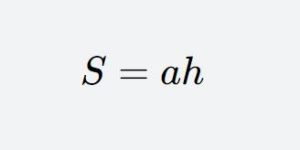
where a is the length of the base, and h is the height.
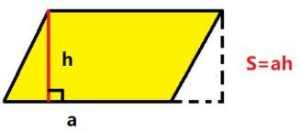
Specifically, the base is one side of the parallelogram, and the height is a line segment perpendicular to the base, whose length is the height of the parallelogram.
2.Core Formula of the Sine Calculation Method
The area S of a parallelogram can be calculated using the lengths of its two adjacent sides a, b, and the included angle θ (pronounced “theta”) between these two sides. The formula is:S=absinθ
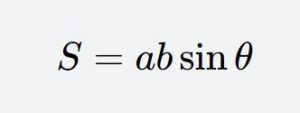
Where:
- a and b are the lengths of the two adjacent sides of the parallelogram respectively;
- θ is the included angle between these two adjacent sides (with a value range of 0∘<θ<180∘);
- sinθ represents the sine value of the included angle θ (which can be found using a calculator or a trigonometric function table).
Explanation of the Principle
The essence of the sine calculation method is to “transform” the parallelogram into a triangle or a rectangle for derivation:
- A parallelogram can be divided into two congruent triangles by its diagonal. The area of each triangle is 21absinθ, so the area of the entire parallelogram is the sum of the two, which is absinθ;
- Geometrically, if side a is taken as the base, the height h of the parallelogram can be expressed as bsinθ (according to the definition of trigonometric functions: sinθ=bh⇒h=bsinθ). Substituting this into the “base-height formula” S=ah, we can also derive S=absinθ.
Application Scenarios
The sine calculation method is more convenient when the lengths of two adjacent sides and the included angle of a parallelogram are known, and it is not easy to directly measure the height. For example:
- Given that the adjacent sides are 5cm and 8cm respectively, and the included angle is 60∘, then the area S=5×8×sin60∘=40×23=203cm2≈34.64cm2.
This formula is essentially consistent with the “base-height calculation method”, but differs in expression. You can choose to use it flexibly according to the known conditions.