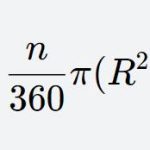Annular Area Calculator
Annuli are common geometric shapes in daily life and engineering—think of washers in mechanical parts, circular decorative patterns in architecture, the data storage area of a CD, or the ring-shaped walkway around a swimming pool. To calculate the area of such ring-shaped structures accurately, we first need to clarify the definition of an annulus, then derive its area formula using basic geometric knowledge, and finally master its practical application.

1. The Mathematical Definition of an Annulus
From a geometric standpoint, an annulus is a closed planar region bounded by two concentric circles (circles sharing the same center) with different radii. This definition relies on two core conditions—neither can be omitted:
- Shared center: The two circles must be “concentric,” meaning they have the same central point. If their centers do not align, even with different radii, the resulting shape is just an “overlapping area of two circles,” not an annulus.
- Unequal radii: The two circles forming the annulus must have different radii. If the radii are equal, the two circles overlap completely, leaving no “ring-shaped region”—so an annulus cannot form.
In simple terms, an annulus can be visualized as “the ring-shaped part left after cutting out a smaller circle from the center of a larger circle.” Its essence is the difference in area between two concentric circles.
2. Foundational Knowledge: The Area Formula of a Circle
Before deriving the annulus area formula, we need to review how to calculate the area of a single circle—since the area of an annulus is essentially the difference between the areas of two circles.
For any circle, if its radius is \( r \) (usually represented by the lowercase letter \( r \)), the relationship between the circle’s area \( S \) (area is denoted by the uppercase letter \( S \)) and its radius is:\( S = \pi r^2 \)
Here, \( \pi \) (pronounced “pi”) is a constant mathematical value, approximately equal to 3.14 (you can use 3.14 for \( \pi \) in calculations unless specified otherwise).
For example, the area of a circle with a radius of 5 centimeters is:\( S = 3.14 \times 5^2 = 3.14 \times 25 = 78.5 \, (\text{square centimeters}) \)
3. Deriving the Area Formula of an Annulus
Based on the annulus’s geometric feature—”a smaller circle cut out from a larger circle”—we can derive its area formula in the following steps:
Step 1: Define Symbols to Distinguish Radii
To avoid confusion, we use the uppercase letter \( R \) to represent the radius of the “larger circle” in the annulus, and the lowercase letter \( r \) to represent the radius of the “smaller circle” (note: \( R > r \)).
Step 2: Calculate the Areas of the Larger and Smaller Circles
Using the circle area formula:
- Area of the larger circle: \( S_{\text{large}} = \pi R^2 \)
- Area of the smaller circle: \( S_{\text{small}} = \pi r^2 \)
Step 3: Compute the Area of the Annulus
Since the area of the annulus equals “the area of the larger circle minus the area of the smaller circle,” we get:\( S_{\text{annulus}} = S_{\text{large}} – S_{\text{small}} = \pi R^2 – \pi r^2 \)
Step 4: Simplify the Formula by Factoring
Looking at the equation \( \pi R^2 – \pi r^2 \), we can factor out \( \pi \) using the distributive property of multiplication, resulting in a more concise formula:\( \boxed{S_{\text{annulus}} = \pi (R^2 – r^2)} \)
Critical Reminder: Avoid Common Mistakes
A frequent error during derivation is miswriting the formula as \( \pi (R – r)^2 \). This is incorrect because \( (R – r)^2 = R^2 – 2Rr + r^2 \), which is entirely different from \( R^2 – r^2 \). Remember the correct order of operations: first calculate the difference between the squares of the radii, then multiply by \( \pi \).
4. Practical Application: An Example of Calculating Annulus Area
Memorizing the formula is not enough—let’s use a specific example to verify how it works, following these clear steps:
Example: Calculate the Area of a Mechanical Washer
A mechanical washer has an annulus shape. Its larger radius \( R = 8 \) cm, and its smaller radius \( r = 5 \) cm. Find the area of the washer (use \( \pi = 3.14 \)).
Calculation Steps:
- Step 1: Calculate \( R^2 – r^2 \)
First, find the square of each radius: \( R^2 = 8^2 = 64 \) (square centimeters), \( r^2 = 5^2 = 25 \) (square centimeters).
Then compute the difference: \( R^2 – r^2 = 64 – 25 = 39 \) (square centimeters).
- Step 2: Substitute into the Formula to Find the Area
Multiply the difference by \( \pi \): \( S_{\text{annulus}} = 3.14 \times 39 = 122.46 \) (square centimeters).
Result:
The area of the mechanical washer is 122.46 square centimeters.
5. Summary and Application Scenarios
1. Key Knowledge Points
- Definition of an annulus: A closed region bounded by two concentric circles with unequal radii.
- Area formula: \( S_{\text{annulus}} = \pi (R^2 – r^2) \) (where \( R \) = radius of the larger circle, \( r \) = radius of the smaller circle).
- Critical operation tip: First calculate the difference between the squares of the radii, then multiply by \( \pi \)—do not mix up the order of operations.
2. Common Application Scenarios
The annulus area formula is widely used in engineering design (e.g., calculating material usage for ring-shaped parts), construction (e.g., finding the floor area of circular flower beds), and daily product design (e.g., the ring-shaped base of a thermos). By measuring the outer radius of the annulus (corresponding to \( R \) in the formula) and the inner radius (corresponding to \( r \)), you can quickly calculate its area to support practical problem-solving.